Managing both extremely large and incredibly small numerical numbers is a necessity for scientific and technical fields. Working with measurements of either extreme is incredibly complex, and it is simpler to work with numbers when they are written in an abbreviated form called scientific notation. This post will serve as a beginner’s guide to the “how” and “why” of scientific notation.
Writing in Scientific Notation
Scientific notation provides a mathematical shorthand to make numbers easier to work with. Why is this necessary? Let’s consider the amount of electrons that go through one ampere (amp) of current. A unit of electrical charge (called a coulomb) that moves through a spot in one second is equal to one amp. By dividing the charge per electron by the charge per amp, we find that there are approximately 6,240,000,000,000,000,000 electrons in one amp. Dealing with that many zero digits can quickly complicate things!
The significant digits of a number (also referred to as significant figures or “sig figs”) are the accurate and precise digits in a measurement or computation that reveal a value’s correctness. For instance, if we say a cement block weighs 5,000 pounds, we likely don’t mean that it weighs exactly 5,000 pounds. Most often, we round the weight to a number that is easier to remember. In this case, the “5” in front would be the only significant digit; and the zeros are just placeholders. However, if we were to claim that the cement block weighed 5,008 pounds, all four digits become significant digits. This is because the weight is no longer rounded to the next thousand pounds- which indicates that the two zeros in the middle are not merely filler digits, but instead represent accuracy. While the zeros in “5,000” are meant to show the scale of the number, the zeros in “5,008” are meant to show the accurate measurement. Any digit in a number that is not zero is always regarded as a significant digit, as well as any zeros in-between nonzero numbers.

This is where scientific notation comes in handy. When writing a number in scientific notation, the “placeholder” zeros are represented by a power-of-ten multiplier. The three distinct sections of scientific notation, are the power, base, and coefficient. For example, 4.6 X 10^7 has a power of 6, a base of 10, and a coefficient of 4.6.
In scientific notation, the number 6,240,000,000,000,000,000 can be represented by moving the decimal point (located at the end of the number) to the left until there is only one nonzero digit to the left of it.
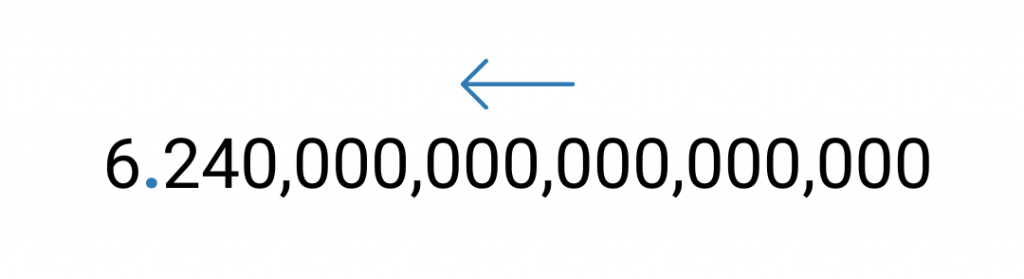
Next, count the number of places the decimal point was moved- in this case, it was moved 18 places.
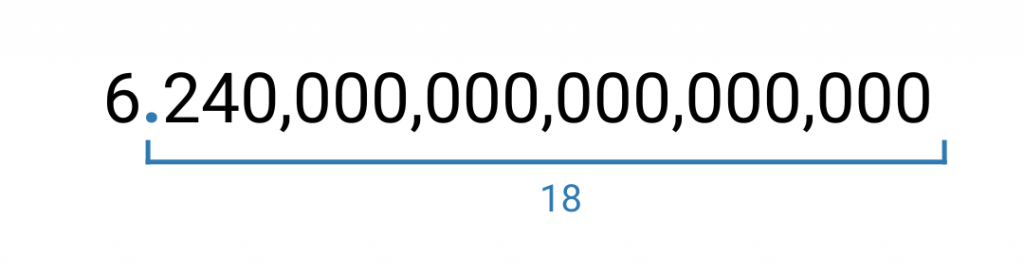
Therefore, in scientific notation, 6,240,000,000,000,000,000 is written as 6.24 × 10^18. 10 to the 18th power indicates 10 multiplied by itself a total of 18 times, which equals 1 followed by 18 zeros.
What About Small Numbers?
Scientific notation can also be used for incredibly small numbers. For example, let’s say that the approximate diameter of a helium atom is 0.0000000000529 meters. In this case, the placeholder zeros are to the left of the significant digits, not the right. To indicate that the decimal should be moved in the opposite direction, we use a negative exponent instead of a positive one.
In this case, 0.0000000000529 becomes 5.29 × 10^-11.

Engineering Notation
Engineering notation offers a unique approach to representing numbers using powers of ten that are multiples of three. This notation is widely used in the field of engineering due to its practicality when dealing with extraordinarily large or small values. This means that the only powers of 10 used in engineering notation are the values 3, 6, 9, 12, etc. These align with common engineering prefixes such as kilo, mega, and giga.
For example, 0.000045 would be written as 4.5 × 10^-5 in scientific notation but would be written as 45 × 10^-6 in engineering notation.
Anyone just beginning to tackle scientific notation should keep a few important notes in mind. In scientific notation, a coefficient should be greater than one but less than 10, and it is always multiplied by a power of 10. The exponent must be either a positive or negative integer that is non-zero. If the exponent is positive, the decimal will be moved that amount to the right, while a negative exponent indicates that the decimal will be moved to the left.
Additional Information