Kirchhoff’s Current and Voltage Laws are at the center of circuit analysis. With them, we have the fundamental tool set we need to start studying circuits and the formulas for individual components such as resistors, capacitors, and inductors. Named after German physicist Gustav Kirchhoff (1824-1887), Kirchhoff’s Laws are electromagnetic approximations derived from Maxwell’s Equations. Simply put, they are applicable when the size of the components in a circuit are substantially smaller than the wavelength of the signals traveling through the circuit.
Kirchhoff’s Current Law
The principle now known as Kirchhoff’s Current Law can be read as “the algebraic sum of all currents entering and exiting a node must equal zero”. A node is a connection between two or more elements. This formula can be written as:
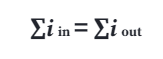
This states that if each current is given an arithmetical sign (or, polarity) indicating whether it enters (+) or exits (-) a node, we can add them up and get a guaranteed total of zero. To put it in more simple terms this law says that the sum of all currents coming into a node are always equal to the sum of all currents flowing out. The law applies to any lumped network, regardless of if it is linear or non-linear, unilateral or bilateral, or active or passive.
Experimental data was used to create both of Kirchhoff’s circuit laws. However, because charge is the product of current and the time it has been flowing, Kirchhoff’s current law may be considered a continuation of the conservation of charge. The current law is based on the assumption that the net charge in wires and components remains constant.

Kirchhoff’s Voltage Law
Discovered in 1847, the principle that has become known as Kirchhoff’s Voltage Law can be stated as: “the algebraic sum of all voltages in a loop must equal zero”. In this statement, algebraic refers to when both polarities and magnitudes are taken into consideration (i.e. the total summation). Any path traced from one point in a circuit around to other places in that circuit and then back to the originating point is referred to as a loop. The voltage total will always equal zero, regardless of where you start tracing the loop or in whatever direction you go. This law can be written as:
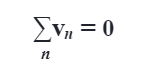
Where n is the number of element voltages throughout the loop.
This law can also be stated as: “the sum of voltage rises equals the sum of voltage drops around a loop.” When written out, it looks like this:
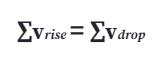
Kirchhoff’s Voltage Law has many interesting attributes. For instance, when it comes to loops, you can start tracing a loop from any node. When you go around the loop and return to the beginning node, the total of the voltages in the loop equals zero- regardless of whether you proceed in a clockwise or counterclockwise direction. This law remains true for each loop in a circuit, even if it has many loops.
If you’re wondering how the element voltages can all be positive when they must add up to zero, consider that the polarity indications and voltage arrows are just voltage reference directions. When the circuit analysis is finished, one or more element voltages around the loop will be negative in relation to the voltage arrow. During computations, the real voltages’ signs always sort out.
The terms “voltage on” and “voltage across” are interchangeable. The resistor has a greater potential at one end than the other. The “voltage across” the resistor is the difference in potential. The nature of resistors is that when a voltage is applied across them, current flows- which results in energy being dissipated.
Some information and formulas in the post are derived from Chapter 6 of “Lessons in Electric Circuits – Volume 1” by Tony R. Kuphaldt under the design science license. https://www.gnu.org/licenses/dsl.html